 |
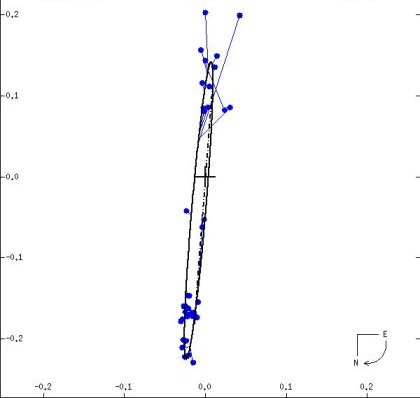
The companion to Theta-1 Tauri orbits its brighter mate (at the cross) every 16.3 years at a mean distance between 9.9 and 10.3 Astronomical Units. A severe eccentricity takes the two from as close as 4 AU to as far as 16. The orbital plane is nearly in the line of sight (the axis inclined by 88 degrees), which results in severe distortion of the actual ellipse and a large displacement of the actual major axis (dashed line). In reality, each orbits the other around a common center of mass. The scale on the axes is in tenths of a second of arc. Compare with Theta-2 Tauri's orbit. From the Sixth Catalog of Orbits of Visual Binary Stars , W. I. Hartkopf and B. D. Mason, US Naval Observatory Double Star Catalog, 2006. |